- Partage ce devoir avec tes amis !
Sujet du devoir
Bonjour, j'aurais besoin d'aide pour ce dm svp.
Un nouveau médicament est très efficace mais présente des effets indésirables dus à un substance agressive pour les cellules sanguines. La modélisation a permis d'évaluer la quantité qn (en cL.L^-1) de substance dans le sang, n heures après l'injection. La substance n'est plus agressive dès que son volume par litre de sang est strictement inférieur à 0.01cL.
On admet que, pour tout n de 
, qn =
1°) A l'aide de la calculatrice , conjecturer la valeur de la substance a très long terme.
2°) déterminer la limite de (qn)
3°) Au début de l'algorithme on effectue la valeur 0 a n, la valeur 2 a q. En fin d'exécution, il renvoie le nombres d'heures nécessaires afin que la quantité de substances n'ait plus d'effet. Compléter cet algorithme
4)Infiquer ce nombre d'heure.
Tant que q ........
n prend la valeur n+1
q prend la valeur ........
Fin Tant que
2 commentaires pour ce devoir
Ils ont besoin d'aide !
- Aucun devoir trouvé, poste ton devoir maintenant.
Bonsoir
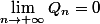
le quotient tend vers 0
on divise par quelque chose de plus en plus grand le résultat va être de plus en plus petit (numérateur tend vers une limite finie le dénominateur vers
intuitivement aussi la quantité va disparaître au bout de quelque temps
sens de variation dérivée signe de la dérivée
puisque il est question de suite * on va montrer que la suite est décroissante
-100(35\text{e}^{n+1}+15)}{(35\text{e}^{n+1}+15)(35\text{e}^{n}+15)}=\dfrac{100\times%2035\text{e}^n(1-\text{e})}{(35\text{e}^{n+1}+15)(35\text{e}^{n}+15)})
)
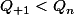suite décroissante
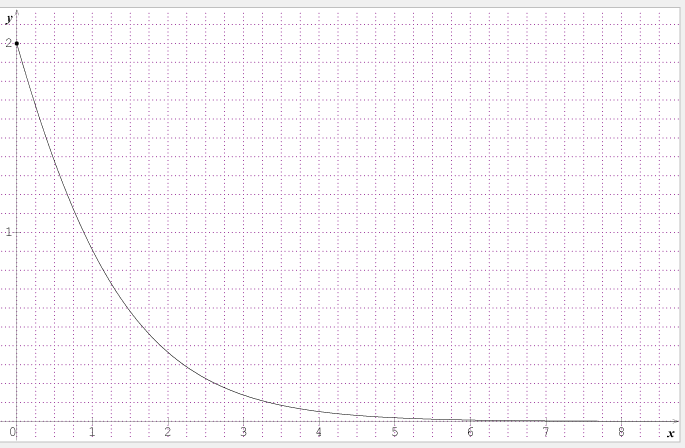
dénominateur positif comme produit et somme de réels positifs numérateur négatif produit d'un nombre positif par un nombre négatif
* il est curieux que la baisse se fasse d'heures en heures et non d'une manière continue
à ce propos la courbe ne devrait avoir que les points à abscisses entières
PS(Je suis en 3eme)
Merci j'avais trouvé ça
juste besoin d'aide pour la 3) et 4)